In order to fly north the plane should orient itself as if it were flying at an angle
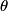 west of north in still air, where west of north in still air, where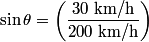 When it does this, the velocity in the northward direction is 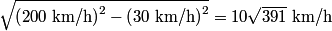 So, the time required to fly 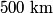 north is north is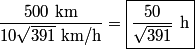 Therefore, answer (D) is correct. |